Ptolemy Lives!
One of the reasons I like old stock certificates so much -- and currency
banknotes too, for that matter -- is the intricate pattern of lines that forms
the borders. These delicate, lacy interwoven lines are a real visual trip, and
there are virtually an endless variety of engraving patterns seen from one
certificate to the next.
I learned that these patterns were made using something called a "geometric
lathe". This machine was invented in the 19th century -- back when people
still knew how to design and build cool mechanical devices! The contraption
pulled an engraving tool over a steel printing plate using a series of
interacting cam wheels whose individual settings created a wonderfully complex
sinusoidal pattern. If you ever used or saw a kid's plastic Spirographtm
toy, I imagine it worked something like that: Wheels turning within wheels.
Look at this example of the border lathework on an old Studebaker-Worthington
stock certificate:
Now, I knew that a point on the edge of one small wheel
revolving around the perimeter of a larger circle describes a figure called an
epicycloid. I have read where some of the geometric lathes using for banknote
printing used as many as 10 separate cam wheels, each with their own settings,
and each influencing the resulting movement all the other wheels -- and,
ultimately, of the engraving tool itself. Figures made from multiple wheels
spinning around each other in this fashion are known as Guilloche patterns.
I played around with creating Guilloche patterns using VisualBasictm.
The heart of the code was the following pair of functions for describing the
point of a drawing pen, as the wheels - 4 of them in my version -- made their
simultaneous turn around a larger "hidden" circle with radius=rada. Each of
the smaller "cam" circles had their own unique radii -- radb, radc, radd, and
rade. The coefficients b, c, d, e served to further "size" the wheels. The
angle, given as "i", is finely incremented around the main circle from 0 to
6.28 (radians, which is the normal angular unit for Basic code).
x = xorg + (rada + radb) * Cos(i) + b * Cos(((rada + radb) / radb) * i) +
c * Cos(((rada + radc) / radc) * i) + d * Cos(((rada + radd) / radd) * i) +
e * Cos(((rada + rade) / rade) * i)
y = yorg - (rada + radb) * Sin(i) - b * Sin(((rada + radb) / radb) * i) -
c * Sin(((rada + radc) / radc) * i) - d * Sin(((rada + radd) / radd) * i) -
e * Sin(((rada + rade) / rade) * i)
I made my code so I could adjust the cam wheel radii and
coefficients using slider bars -- in my mind's eye I imagined those 19th
century engraving machine operators turning big metal cranks to do the same
thing. I also added the capability of repeating the drawing cycles a desired
number of times, with all the radii (including the main circle radius)
shrinking at each pass.
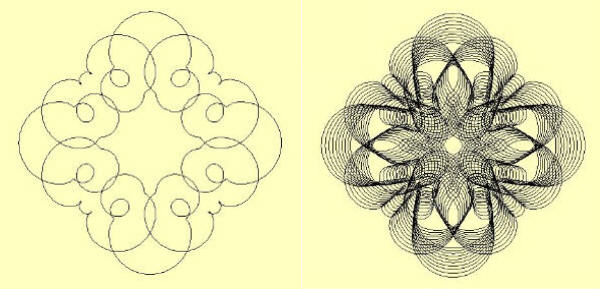
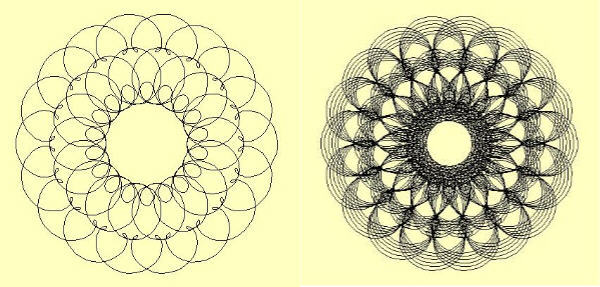
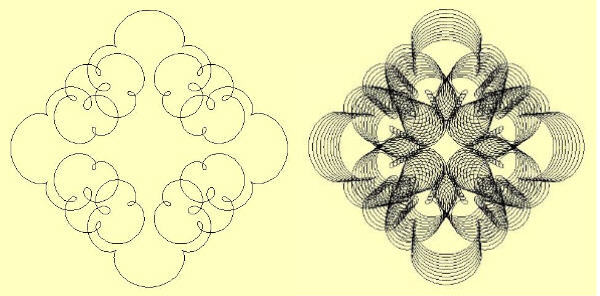
Here are a few typical program outputs, showing a first image with single pass
around the central "hidden" circle, and an image adjacent to it showing
multiple passes around the circle with shrinking radii on each pass. Looking
at the results, I reckon you might could also call this a "doily making"
programů
Postscript: Ptolemy (aka Claudius Ptolemaeus)
was a Greek who lived in Alexandria, Egypt from approx. 87 -150 AD. He
developed a system of epicycles -- small circles revolving around larger
circles -- to account for the apparent planetary motions (particularly
retrograde motion) in an earth-centered model of the solar system. Ptolemy's
system used at least 80 epicycles to explain the motions of the Sun, the Moon,
and the five planets known in his time. It remained the accepted wisdom until
Copernicus and Kepler finally developed the heliocentric model.
Ptolemy's system was actually more accurate than Copernicus' original 1543
version, and his model continued to give the best results until Kepler later
introduced the (proper) notion of elliptical planetary paths in 1609.
Hmmm, that's a theory that stood up well for almost 1500 years. Short of
Aristotle, I don't know of many other human beings that can boast of that
accomplishment. I'll wager not many modern scientific theories will
remain that intact by the year 3500. (It'd be nice to be around to
collect the bets...)
