On another page, I introduced the
Plank length in my musings about how many Wheeler-Everett "Many World"
universes could have evolved since the beginning of time. The Planck length is
1.616 X 10-35 meters long. That’s about 1 ten-octillionth the
diameter of an atom.
The Plank length was conceived by Max Planck in 1899, in his attempt to
establish "natural units" of mass, length and time. (He didn’t name it after
himself, of course; others did.) The Planck length is actually derived from
the Planck mass, which -- forgive me for the technical divergence here –
calculates the mass at which the Schwarzschild radius (the size of a body’s
Black Hole event horizon) is the same size as its quantum-mechanical Compton
wavelength (the spread of a particle’s wave-function). Well, hmmmm. It all
ends up saying that the Planck mass – which is roughly equivalent to the mass
of a largish biological cell – can become a Black Hole if it’s compressed to
the size of a Plank length.
The Planck length has become a very important player in modern physics,
because it describes the size at which quantum mechanical and relativistic
effects become equal partners in determining how things behave. This is the
domain where quantum mechanics happen, where the universe changes from a
smooth analogic continuum to a grainy region, where all events occur in sudden
jumps with no intervening transitions. There is no physical reality to any
length smaller than the Planck length. (My gosh, who would need a smaller
space than 1 ten-octillionth the diameter of an atom to define the
basic dimensional building block of the universe?)
In my calculation of possible Many Worlds universes, I figured the number
of Planck-length volumes that would fit inside the universe, considered (with
present knowledge) as a sphere of diameter 1026 km. I assumed the
Planck volumes to be little cubes, one Plank
length
on a side. That was OK for the purposes of what I was doing at the time, but
it’s definitely unsatisfactory when you think about it more. Surely, a real
Planck volume must be a sphere, not a cube. You can’t accept a "quantum
passage" through a Planck region that’s larger than a Planck length –
certainly not a diagonal trip through from one cube vertex to another, which
would be significantly longer -- 1.732 times longer, in fact -- than along the
side of a cube one Planck length long.
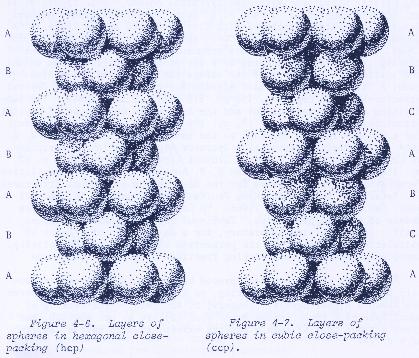
Now this is a real dilemma. You can close-pack cubes, but you can’t
close-pack spheres. There are only 2 ways to pack spheres tightly: a
cubic-centered packing (ccp), or a hexagonal-centered packing arrangement (hcp).
In either case, the packing density, using unit-diameter spheres, is pi/181/2
= 0.7408… There’s a significant amount of space left over. And in the
3-dimensional geometry of our universe, you can’t just pretend that 26%
of the unfilled space is really there and usable for quantum events to occur
inside of.
Now, I suppose you could say that geometry may change at the Planck length
level; that somehow, at that magnification, the diagonal through a cube is
equal to the side length, or that the spheres of Planck-length diameter can
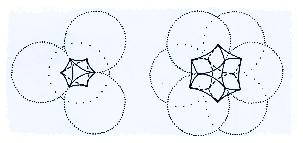
close-pack. That doesn’t seem satisfactory to me. It makes better sense to say
that the concave-planar octahedronal and cuboctahedronal solids that
correspond to the empty spaces between the close-packed Planck unit spheres
are not to be considered part of the universal volume, and in fact don’t exist
at all except as small houses for wee ghosts:
Quantum mechanics obey the laws of general relativity, and they also obey "localistic"
physical laws. The flow of information derived from any quantum mechanical
transaction is limited by the speed of light in a vacuum. (Another way of
saying this is that it must remain within the ever-expanding Minkowski
light-cone that marks out the boundaries of our universe.) We normally
consider the path of a photon as being a straight line – except when
influenced by local gravity or by the curvature of space itself. But consider
that a photon has to be recapitulated -- reborn -- within every single
Planck-volume it "passes through". (I believe the quantum odds say that
almost surely a photon going in one side will still be a photon coming out
the other.) In a cubic-centered packing, each Planck sphere is surrounded and
contacted, at one point on its surface, by 12 others. The contact points in a
large set of close-packed spheres don’t line up in a straight line. Therefore,
it seems unavoidable that the photon’s trip must consist of a series of
doglegs from the original angle of flight, dictated by wherever the contact
points between adjacent Planck-spheres occur which are closest to the original
photon incidence angle. It’s not permissible to talk about "increments of
travel" less than one Planck length long, so you have to presume that the
travel length of a photon "through" each Planck volume must be exactly 1
Planck length long -- that is, a virtual journey from the outer contact point
to the center of the sphere, plus the virtual journey to another surface
contact point that is the closest one to the photon’s original incidence angle
vector – the angle as if the photon were to go "straight through" the sphere.
Here is a 2-d representation of what I am talking about:
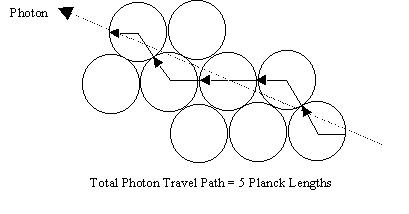
Or, as an alternate, here is another representation that allows the photon
to "jump across" the concave-planar octahedronal and cuboctahedronal gaps
between the Plank volume-spheres (since we earlier established that these were
not considered part of the universe's volume, remember?):
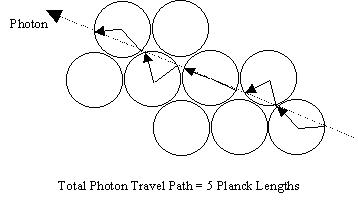
In either case, the photon trip length is the same, 5 Planck lengths long.
(I won't speculate here on how, in either example, the photon knows exactly
where on the circumference its original bearing line enters or exits!)
Of course, in these 2-d representations, there are incidence angles which
produce a "straight-through shot", where the scalar length is equal to the
number of Planck lengths traversed. I think that’s not the case in a 3d
packing arrangement, however.
You can see there are a number of alternate paths from one end to the other
which yield the same total photon Planck travel length. That’s true in the 3d
scenario also.
The number of Planck-lengths between two points cannot simply be their
scalar straight-line distance divided by the Planck length. That's
because Planck volumes, which have to be considered as an arrangement of
close-packed spheres, don’t line up nicely along any straight line. You
can’t have a fractional Planck length, so you have to calculate the length as
the total integer number of close-packed Planck spheres laying between the two
points. That will always be a greater number than the straight scalar
distance, since packed spheres must jigger themselves in all 3 spatial
dimensions to nest properly. I would hazard a guess that the actual
"Plank scalar length" would be some function of the inverse of the ccp
packing density number, perhaps a cube root of that, and rounded up to the
next whole integer, e.g., int(scalar length * 1/(.7408))^1/3 + 1)
or something like that.
In other words, as the crow flies, the photon tarries. The further away the
origin of the photon, the tardier it will be in reaching us. The Planck
time unit is the time it takes for light to travel the distance of one Planck
length -- 10-43 seconds, to be precise. As with the Planck
length, there is no physical meaning to time durations less than the Plank
time. The photon has to navigate through each Planck unit volume it
encounters -- that is, it has to take a full Planck time unit to pass it,
regardless of how short the imaginary chord through the Planck sphere is, that
describes the photon's original bearing. (Remember, you can't talk about
any lengths shorter than a Planck length!) But our imaginary specular
crow can "cut the corners", so to speak. Were he also to be traveling at
the speed of light, he would get to his destination much, much quicker than
the poor plodding photon.
I’ve heard criticisms of physicists' explanations of the spectrographic
frequency "red shift" (Doppler Effect) phenomenon that cosmologists use to
base the size of the universe upon. Some alternate (mostly crackpot)
explanations talk about "tired light" causing the apparent shift. Maybe those
distant photons are indeed tired, after having to zig-zag their way
through so many Planck-volume spheres to reach us. (And if the size of the
universe and the speed of light is flummoxed up, maybe the universe really
was created by God in October 4004 BC, as Bishop Usher so craftily
calculated long ago. And maybe it’s not so big after all.)
One problem (among many) with this thought experiment is how a photon can
"remember" its original bearing as it passes through the complex network of
intervening Planck volumes. As it enters any individual Planck volume, its
exit point could be any one of 12 adjacent sphere contact points (including
its original entry point) -- with no energy penalty at all associated with any
of the 12 possible exit choices. If you consider that a photon has so many
degrees of freedom at every Planck volume sphere it passes through, it’s hard
to imagine how any photons at all get from the thing I am looking at to
my eye. Conversely, many photons emanating from other, completely different
objects would end up winding their way into the Planck volume-network path to
my retina, interfering with the thing I’m supposed to be looking at.
Plus, what exactly does "photon incidence angle" or "original bearing"
mean? The photon itself originated in a close-packed Planck sphere, and
if that’s the case, then it would be constrained to have only one of 12 total
exit incidence angles!
Maybe those wee ghosts that live in the ("shall-not-be named,
but-I-did-it-anyway") concave-planar octahedronal and cuboctahedronal gaps
between the Plank volume-spheres contribute an essential service by
shepherding photons through their neighboring Planck sphere-fields.
Afterwards, work done, perhaps they meander down to the neighborhood
cuboctahedronal pub to imbibe a pint or two. Stranger things have been
postulated in the annals of Physics...
These problems arise if one considers the Planck volume packing arrangement
to be static. But nothing appears to be static in the universe; all the
physical events that we can observe are characterized as a teeming, writhing,
seething, vibrating, foaming condition of constant change. If the Planck
universal volume packing also jiggles, then perhaps the "lowest energy
solution" of a photonic journey through it is more selective and directive. In
quantum mechanical terms, perhaps the probability wave function in that
scenario would favor a photon's exit point from a Planck volume sphere that is
more correlated with its original entry incidence angle. However, I can’t
think of a definite reason why that would be the case, so I’m not completely
convinced that jiggling would solve anything. After all, I myself jiggle
a lot more than I used to, and it hasn't done me any good at all...
Back to Lost Articles...
The sphere packing images are from The Geometrical Foundation of Natural
Science, Robert Williams (Dover, 1979). I can’t even begin to count the
times I’ve gone back to this book as reference material for all sorts of
different things.
I have no real problem with the physical theory behind the Doppler
(red-shift) effect, except for the common example always given to illustrate
it. That is the one about the train whistle, that seems to drop in pitch
as the train rushes past and away from you. It's much more likely that
the perceived pitch drop is due to the decline in sound magnitude (amplitude),
not by a drop in frequency. Anybody who listens to music using
headphones knows that if you move the headphones further away from your ears,
the song pitch appears to drop. This is strictly an auditory-perceptual
phenomenon, not a Doppler Effect. When the amplitude of an auditory
sound signal drops, the pitch -- as perceived and interpreted by the human
brain -- also drops.
The following information on the Planck realm is excerpted from The Vacuum,
Light Speed, and the Redshift, by Australian Astronomer Barry Settlefield (http://www.ldolphin.org/setterfield/vacuum.html).
I should point out that Mr. Settlefield's ideas are generally
discredited within the scientific community as being "bad science", and Settlefield himself is associated with the
conservative Christian Creationist movement. But the
background information in the early part of this paper is a quite well-written
review for the layman of accepted modern physical theory relating to this
subject -- as far as it goes:
"…When dealing with the vacuum, size considerations are all-important. On
a large scale the physical vacuum has properties that are uniform throughout
the cosmos, and seemingly smooth and featureless. However, on an atomic
scale, the vacuum has been described as a "seething sea of activity", or
"the seething vacuum". It is in this realm of the very small that our
understanding of the vacuum has increased. The size of the atom is about 10-8
centimeters. The size of an atomic particle, such as an electron, is about
10-13 centimeters. As the scale becomes smaller, there is a major
change at the Planck length (1.616 x 10-33 centimeters), which we
will designate as L. In 1983, F. M. Pipkin and R. C. Ritter pointed out in
Science (vol. 219, p.4587), that "the Planck length is a length at which the
smoothness of space breaks down, and space assumes a granular structure."
This "granular structure" of space, to use Pipkin and Ritter's phrase, is
considered to be made up of Planck particles whose diameter is equal to L,
and whose mass is equal to a fundamental unit called the Planck mass, M,
(2.177 x 10-5 grams). These Planck particles form the basis for
various cosmological theories such as strings, super strings, 10-dimensional
space, and so on. During the last hundred years, physicists have discovered
that atomic particles such as electrons or protons, have a wave-form
associated with them. This is termed the wave/particle duality of matter.
These waves are called de Broglie waves and vary inversely with mass. That
is to say, the heavier the particle, the shorter its wavelength. This means
that because a proton is more massive, its wavelength is shorter than an
electron's. What is interesting and important is that Planck particles have
a diameter L that is equal to their de Broglie wavelength.
The physical vacuum of space therefore appears to be made up of an
all-pervasive sea of Planck particles whose density is an unbelievable 3.6 x
1093 grams per cubic centimeter. It might be wondered how
anything can move through such a medium. It is because de Broglie
wavelengths of elementary particles are so long compared with the Planck
length, L, that the vacuum is 'transparent' to these elementary particles.
It is for the same reason that long wavelength infrared light can travel
through a dense cloud in space and reveal what is within instead of being
absorbed, and why light can pass through dense glass. Therefore, motion of
elementary particles through the vacuum will be effortless, as long as these
particles do not have energies of the magnitude of what is referred to as
Planck energy, or M* c2 ('c' is the velocity of light). Atomic
particles of that energy would simply be absorbed by the structure of the
vacuum. From the figures for the density given above, the energy associated
with this Planck particle sea making up the physical vacuum can be
calculated to be of the order of 10114 ergs per cubic centimeter.
This is the maximum value for the "Zero Point Energy" (ZPE) inherent in the
vacuum..."
"...In order to appreciate the
magnitude of the ZPE in each cubic centimeter of space, consider a
conservative estimate of 1052 ergs/cc. Most people are familiar
with the light bulbs with which we illuminate our houses. The one in my
office is labeled as 150 watts. (A watt is defined as 107
ergs per second.) By comparison, our sun radiates energy at the rate
of 3.8 x 1020 watts. In our galaxy there are in excess of 100
billion stars. If we assume they all radiate at about the same intensity as
our sun, then the amount of energy expended by our entire galaxy of stars
shining for one million years is roughly equivalent to the energy locked up
in one cubic centimeter of space."
I don't know why or if each
Planck-length unit sphere can truly be considered to be a "Planck particle of
Planck Mass". Since a particle of such characteristics and size turns
out to be a Black Hole, that would mean that the Universe is packed tightly
with Black Holes! But the concept of ZPE itself seems to be valid in the
general scientific community. See
http://www.calphysics.org/zpe.html.
